素因数分解を使った入試問題
中学の数学で勉強をした素数や素因数分解を覚えていますか?
忘れてしまった人はまずはこちらで復習してみましょう!
素数
youtu.be
素因数分解
youtu.be
素数を使った計算は高校入試の定番問題です。たとえば、今年(令和2年)の神奈川県公立高校入試問題ではこんなものが出ました。
この問題を解きます。

この問題の正答率は72.3%でした。この年の数学の平均点は、55.7点ということですので、受験生としては確実に正答にしたい問題だったと思います。
![]()
エラトステネスの篩
素数は中学で習う基本的な数学ですが相当、奥が深い分野です。それは、素数を求める公式が見つかっていないことに起因します。
素数を求める一番有効な方法は「エラトステネスの篩(ふるい)」と呼ばれる方法です。これは素数を求めたい整数を一覧にして素数の倍数を消していきます。そこで残った数が素数という消去法です。
下の図は100までの素数を求める方法です。100は10×10ですので、この場合は10以下の素数のみを倍数にして、その値を消去すればよいことになります。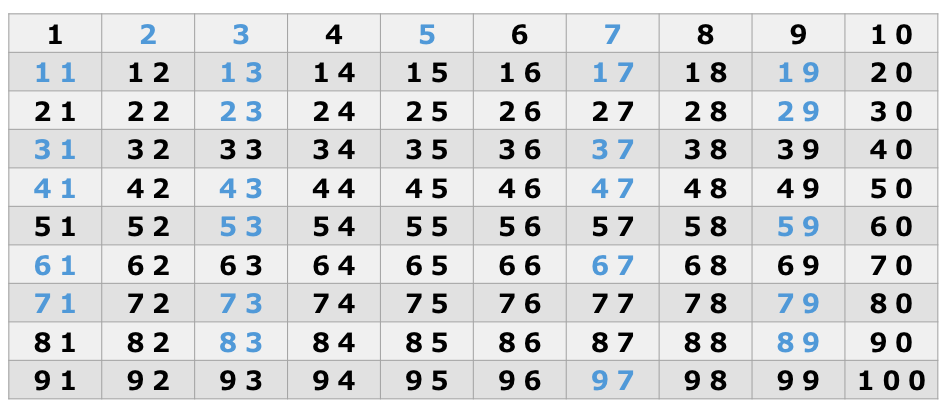
- 2の倍数は素数でない:4→6→8→10→12→14→16→18→20→22→24→26→28→30→32→34→36→38→40→42→44→46→48→50→52→54→56→58→60→62→64→66→68→70→72→74→76→78→80→82→84→86→88→90→92→94→96→98→100
- 3の倍数は素数でない:6→9→12→15→18→21→24→27→30→33→36→39→42→45→48→51→54→57→60→63→66→69→72→75→78→81→84→87→90→93→96→99
- 5の倍数は素数でない:10→15→20→25→30→35→40→45→50→55→60→65→70→75→80→85→90→95→100
- 7の倍数は素数でない:14→21→28→35→42→49→56→63→70→77→84→91→98
エラトステネスは古代ギリシャの学者です。この方法より、効率的に素数を求める方法は未だ存在していないのです。
RSA暗号
RSA暗号は大きな数の素因数分解の困難性を利用した暗号方式です。
たとえば、2つの大きな素数を並べます。
- 素数その1:524287
- 素数その2:131071
この二つの掛け算は簡単です。
- 524287×131071=68718821377(簡単)
しかし、68718821377という数字を素因数分解することは非常に困難です。
- 68718821377=524287×131071(困難)
この性質を利用した暗号方式がRSAです。現在の安全な鍵長は2048ビット以上です(使用推奨期間は2030年まで)。
RSAは公開鍵暗号の署名アルゴリズムで推奨されているリスト(CRYPTREC電子政府推奨暗号リスト)として掲載されています。
| 名 称 | アルゴリズム |
|---|---|
| DSA | エルガマール暗号 |
| ECDSA | 楕円曲線暗号 |
| RSASSA-PKCS1-v1_5 | RSA暗号 |
| RSA-PSS | RSA暗号 |
PCI DSS
クレジットカード業界では、個人の金融情報を扱っています。オンライン化による利便性の追求と共に高いセキュリティへの配慮が重要です。安全性の高いRSA暗号はクレジットカード会社に重宝され、会員データの保護に使われています。
- カード会員データを保護するために、ファイアウォールをインストールして構成を維持する。
- システムパスワードおよび他のセキュリティパラメータにベンダ提供のデフォルト値を使用しない。
- 保存されるカード会員データの保護する。
- オープンな公共ネットワーク経由でカード会員データを伝送する場合、暗号化する。
- アンチウィルスソフトウェアまたはプログラムを使用し、定期的に更新する。
- 安全性の高いシステムとアプリケーションを開発し、保守する。
- カード会員データへのアクセスを、業務上必要な範囲内に制限する。
- コンピュータにアクセスできる各ユーザに一意のID を割り当てる。
- カード会員データへの物理アクセスを制限する。
- ネットワークリソースおよびカード会員データへのすべてのアクセスを追跡および監視する。
- セキュリティシステムおよびプロセスを定期的にテストする。
- すべての担当者の情報セキュリティポリシーを整備する。
量子コンピュータの登場により、高い安全性を持つ暗号も危殆化するといわれます。技術の進歩は喜ばしいことですが、セキュリティ対策がそこに追いつけるかは課題です。